The Quantum Whole
The Cosmic Population of Primal Cells
The universe consists of an invariant large number of identical cellular objects N, that must exist in one of two quantum physical states, the a-state or the b-state.
N a-state + N b-state = N cosmos
The two states can be topologically combined through natural phenomena, such as stars, to create two additional physical states, the ab-state and the abb-state. These interactions between the physical properties of just these four physical states – two quantum and two topologically combined – are sufficient to explain the structure of the atoms.
A simple way of looking at the two quantum states is to visualize them in the form of an invariant large number of identical cosmic eggs.
● The a-state is the whole egg made up of three forms of matter, analogous to the yolk (core), the shell (membrane), and the white (plasm).
The a-state is the ordinary neutron
● The b-state is the broken egg, where the neutron core becomes the proton core, the neutron membrane becomes the electron ball, and the neutron plasm becomes the four forms of environmental energy: electricity, space, motion, and light.
The b-state is ordinary hydrogen
Neutron Structure
The neutron is the quantum whole of nature with the topology of an egg.
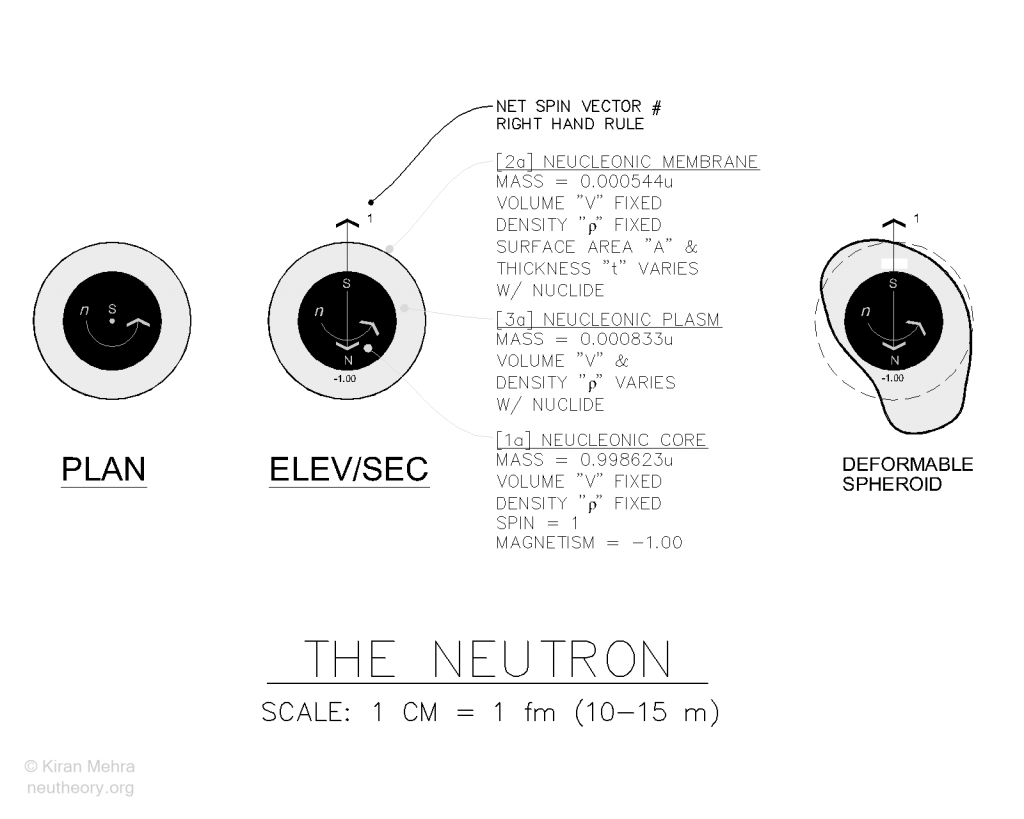
The a-state neutron cell has five intrinsic parts. Each part is a fundamental physical form of nature. The Neu Theory description of nature starts with these five forms.(Throughout the work a number in this type of brackets [#], refers to one of the fundamental physical forms of nature, e.g., [1] is the spinrise core.):
- [1a] spinrise core
- [2a] spinrise membrane
- [3a] spinrise plasm
- [4] g-spin/magnetism
- [5] g-rise/spinfield
The first three fundamental physical forms of nature [1a][2a][3a] are forms of matter made by the primal linkage of 939.565 379 MeV spin movement/energy with 939.565 379 MeV rise movement/energy making 1.674 929 351 x 10-27 kg of spinrise mass.
- There are two types of matter in nature:Type I matter is a fixed density spinrise substance. Type I matter forms:
- core matter [1a][1b].
- membrane matter [2a][2b].
- Type II matter is a variable density spinrise substance. Type II matter forms:
- plasm matter [3a] only.
Each of the three forms of matter carries a fixed proportion of the whole (quantum) mass which is set equal to 1.000 000 neu. The model uses this as an absolute value, and as the atomic mass unit (amu).
The fourth and fifth fundamental physical form of nature, g-spin/magnetism [4] and g-rise/spinfield [5], are forms of movement/synergy that result from the intrinsic physical acceleration of matter.
The free neutron cell also carries the ninth fundamental physical form of nature, motion [9], which is directly related to its overall physical size. Faster neutrons are smaller, slower neutrons are larger.
The free neutron cell is naturally unstable and will spontaneously transform into b-state ionic hydrogen with an average lifetime of approximately 15 minutes. The Neu Theory model calls this transformation the little bang, current science calls it “beta decay”. (See 4.1).
The SpinRise Core
The spinrise core is fundamental physical form of nature [1] in the Neu Theory model.
Topologically similar to the yolk in the egg analogy, the neutron cell core, is a perpetually spinning ball of homogeneous spinrise substance at an absolute density (Type I matter). The right hand spin axis provides primary reference.
- mass = 1.672 622 x 10-27 kg. This represents ≈ 99.86 % of quantum mass.
- volume = 2.499 x 10-45 m3 (1.68368 x 10-15 meters diameter ball)
- density = 6.693 x 1017 kg/m3
- g-spin = period 1.764 x 10-23 seconds, frequency 5.667 x 1022 cycles per second
- g-rise = 1.57×10-7 m/s2
The fixed mass and volume of the spinning spinrise core [1a], results in a calculated absolute density of 6.693 x 1017 kg/m3, making core Type I matter incredibly dense stuff, the maximum density allowed by nature.
To give some human scale meaning to how truly dense this is – were it possible to make a one centimeter cube of pure core matter, the size of a small sugar cube – it would have a mass of approximately 6.69 x 1011 kg which is more than the combined mass of two hundred thousand (200,000) Empire State Buildings!
The spinning spinrise core behaves as a homogenous incompressible solid mass, but can fragment if hit hard enough. Visualize the behavior of a drop of elemental mercury. When struck, it breaks into smaller droplets.
The SpinRise Membrane
The spinrise membrane is fundamental physical form of nature [2] in the Neu Theory model.
Topologically similar to an eggshell, the neutron cell membrane, is a non-spinning layer of homogenous spinrise substance at an absolute density (Type I matter), that contains the cell plasm, which completely surrounds the spinning core. In stable nuclides, the non-spinning membranes and spinning cores do not touch each other, as there is always some plasm between the S1 & S2 surfaces.
- mass = 0.911 x 10-30 kg. This represents ≈ 0.05 % of quantum mass.
- volume = 2.499 x 10-45 m3
- density = 6.693 x 1017 kg/m3 (same as the core)
- diameter = varies: 1.96 x 10-15 m (Pb208); 2.88 x 10-15 m (Li7); 1.0 x 10-7 m (UCN)
- thickness = varies: 11.08 x 10-20 m (Pb208); 5.12 x 10-20 m (Li7); 4.3 x 10-35 m (UCN)
- g-rise = varies: with overall neutron size
The average cell diameter, and sheet thickness, of the spinrise membrane [2a] stabilizes for each nuclide. (See Neu Mass & Charge Radii Table – Columns AZ and BG). For free neutrons, the cell diameter and sheet thickness, varies with their speed of motion.
The cell spinrise membrane behaves somewhat like a liquid rubber film. Similar to a rubber balloon filled with a compressible gas, we can imagine it expanding, contracting, or deforming in shape as needed, to best fit the available volume within a nuclide. However, unlike a rubber balloon, it is hypothesized that there is no “tension” in the film as the thickness changes. Membrane matter can make “sharp corners” in a nuclide. The physical volume of the membrane spinrise substance remains constant at an absolute density.
The free neutron cell can reflect (bounce) off a suitable surface. For example, a narrow beam of neutrons is made to strike a “flat” surface at a very slight angle. Instead of being absorbed, the neutrons will bounce off the surface, similar to the reflection of light or a ping-pong ball, and keep on moving in space, until they transform, or are absorbed by some nuclide.
The thickness of the cell membrane sheet varies with the overall size of the neutron. A free “cold” neutron, with a diameter of 3 x 10-11 m, has a calculated sheet thickness of 4.5 x 10-28 m. A free “ultra cold” neutron (UCN), with a diameter of 1.0 x 10-7 m, has a calculated sheet thickness of 4.3 x 10-35 m, a very gossamer sheet of liquid spinrise indeed.
Remarkably, the absolute density of the spinrise sheet never varies, and is hypothesized to remain a constant 6.69 x 1017 kg/m3!
This unimaginable coherent thinness, of the spinrise cell membrane of an UCN neutron, approaching the Planck length – 20 orders of magnitude smaller than the proton radius – is in fact required by the conservation of the law of form, because the S2-S3 surfaces making up the membrane must remain topologically “complete.” The physical effect of topological homogeneity maintains a coherence of shape by the membrane, despite large changes in size. This requires us to think of matter in a very different manner.
The SpinRise Plasm
The spinrise plasm is fundamental physical form of nature [3a] in the Neu Theory model.
Topologically similar to an egg white, the neutron cell plasm, is a fixed amount of non-spinning homogenous spinrise substance with a variable density (Type II matter), that expands or contracts to completely fill the containment volume, defined by the core S1 surface and the membrane S2 surface.
- mass = 1.395 x 10-30 kg. This represents ≈ 0.08 % of quantum mass.
- volume = varies: 1.44×10-45 m3 (Pb208); 36.20×10-45 m3 (H2); 4.19×10-21 m3 (UCN)
- density = varies: 9.68×1014 kg/m3 (Pb208); 0.39 x1014 kg/m3 (H2); 3.33 x10-10 kg/m3 (UCN)
The cell plasm [3a] does not have any topological surfaces of its own to give it independent shape. It is a contained physical volume defined by the S1 ball surface of the core and the S2 hollow surface of the membrane. It is a fixed amount of matter, with a volume that varies, with the shape and size of its container. This behavior is somewhat analogous to a gas, except that the cell plasm is considered one homogenous object, unlike the large (but finite) number of individual molecules of a contained gas.
As the neutron cell diameter gets larger, the contained volume increases and the density of the cell plasm matter homogeneously decreases. As the neutron cell diameter gets smaller, the contained volume decreases and the density of the cell plasm matter increases. This variable density substance is called Type II matter, and is different from the Type I matter of the core and membrane forms, where the volume and density always remain constant.
Of all the nuclides, the densest cell plasms are with the 126 cells of Lead 208, each of which has a volume at 1.44 x10-45 m3 – the smallest plasm volume in nature. The calculated plasm density of Pb208 at 9.68×1014 kg/m3, is approximately 689 times less than the absolute density of core and membrane matter. This is still, the mass of over two hundred and ninety (290) Empire State Buildings, in a 1 cm cube. The cell plasms of all other atomic nuclides, have larger volumes and are correspondingly less dense.
The nuclide with the least dense cell plasm is the deuteron (H2) neucleon, which has a volume of 36.20 x10-45 m3 and a density at 0.39 x1014 kg/m3. This is over 17 thousand times less than absolute density yet still extremely dense. One cubic centimeter of deuteron cell plasm would contain the mass of “only” twelve (12) Empire State Buildings.
The least dense cell plasms found in nature are with free unstable “ultra-cold” neutrons (UCN). For example, a 1.0 x 10-7 diameter free neutron cell has a plasm volume of 4.19 x 10-21 m3, with a calculated density at 3.33 x10-10 kg/m3. One cubic centimeter would contain approximately three one millionth (0.000 003) of a gram of matter. The difference between the least and the greatest neutron plasm matter densities spans an amazing 27 orders of magnitude.
However, even the cell plasm density of ultra-cold neutrons, is huge compared to the density of the space they briefly embed until spontaneous transformation. In the Neu Theory model, in principle there can be no space within the body of a neutron, despite the large size. The mass equivalent density of space rise energy, is estimated to be 2.03 x 10-31 kg/m3, 21 orders of magnitude less than the least dense cell plasm.
