Architecture of The Nuclides
The Nuclides
Nature is made of atoms.
The first 238 atoms are the naturally occurring elements and isotopes. Atoms up to Bismuth-209, with the exceptions of mass numbers 5, 8, 147, and 149, are found in stable structures.
Atoms with mass numbers above 209, are all unstable (radioactive), with an average lifetime from less than a microsecond, to billions of years. Radioactive atoms with mass numbers beyond 266, have been made in man made nuclear reactions.
The atomic elements are made by the fusion of deuteron charge shells with each other. The deuterons, and their uncharged neutron guests, remain as a contained cluster of discrete cells, below a charge shield, with their individual physical properties adding together after fusion has taken place.
Neu Theory maintains that without deuterons, there would be no atoms beyond hydrogen. With the exception of the neucleon helium-3, which is a neutron cell with 3 cores and +2 charge shield, the atomic number “Z” of all stable nuclides, is the deuteron number. There are no free protons within a nuclide, they are all captive to deuteron and helion neucleon cells.
Once deuterons (ab) are synthesized they can fuse together into multiple (ab) clusters.
First fused are helium-4 (2ab) and lithium-6 (3ab), but deuterons cannot fuse into beryllium-8 (4ab) without the addition of a neutron (a), as the only stable cluster is beryllium-9 (4ab+a).
A proton (b) is captured by a deuteron (ab) making a helion (abb) (Figure 4.4 – The Three Neucleons) which then can capture an electron making a triton (ab+a) (Figure 4.7 – Neutron Synthesis).
The triton (ab+a) with its +1 charge shield can then fuse with the +3 charge shield of lithium-6 (3ab) to make beryllium-9 (4ab+a) with its +4 charge shield. This is one method by which the only stable isotope of beryllium is synthesized. Another possibility is the deuteron (ab) with its +1 charge shield can fuse with the +3 charge shield of lithium-7 (3ab+a) to make beryllium-9 (4ab+a) with its +4 charge shield.
All even deuteron number nuclides starting with helium-4 (2ab) until calcium-40 (20ab), with the exception of beryllium-9 (4ab+a), have stable cell clusters without a neutron. After a stable 20 deuteron cell cluster (calcium-40), all nuclides need one or more neutron cells to maintain a stable cluster.
All odd deuteron number nuclides after nitrogen-14 (7ab) need one or more neutrons to make a stable cell cluster.
Boron-10 (5ab), carbon-12 (6ab), nitrogen-14 (7ab), oxygen-18 (8ab) are all stable.
Only fluorine-19 (9ab+a) is stable. Neon-20 (10ab) is stable. Only sodium-23 (11ab+a) is stable. Magnesium-24 (12ab) is stable. Only aluminum-27 (13ab+a) is stable. Silicon-28 (14ab) is stable. Only phosphorous-31 (15ab+a) is stable. Sulfur-32 (16ab) is stable. Chlorine is only stable with neutrons (17ab+a, 17ab+3a). Argon-36 (18ab) is stable. Potassium is only stable with neutrons (19ab+a, 19ab+2a, 19ab+3a). Calcium-40 (20ab) is stable.
Neutrons are made in stars in three steps:
- Deuterons are synthesized in a dense, hot hydrogen plasma in the stellar core.
- A deuteron (ab) with a +1 charge shield fuses with a proton (b+) to make a helion (abb) with a +2 charge shield.
- The +2 charge shield helion (abb) captures an electron (e-), losing a +1 charge shell to make a triton (ab+a) with a +1 charge shield. A triton is a two neucleon cluster, a deuteron (ab), and a neutron (a), below a common +1 charge shield.
Nuclide Size
(Figure 4.8 – Relative Charge Radii) is a schematic drawing drawn to scale, except as noted, showing the relative size of selected nuclides. The scale of the drawing is 1 centimeter (cm) = 1 femtometer (fm) (10-15m).
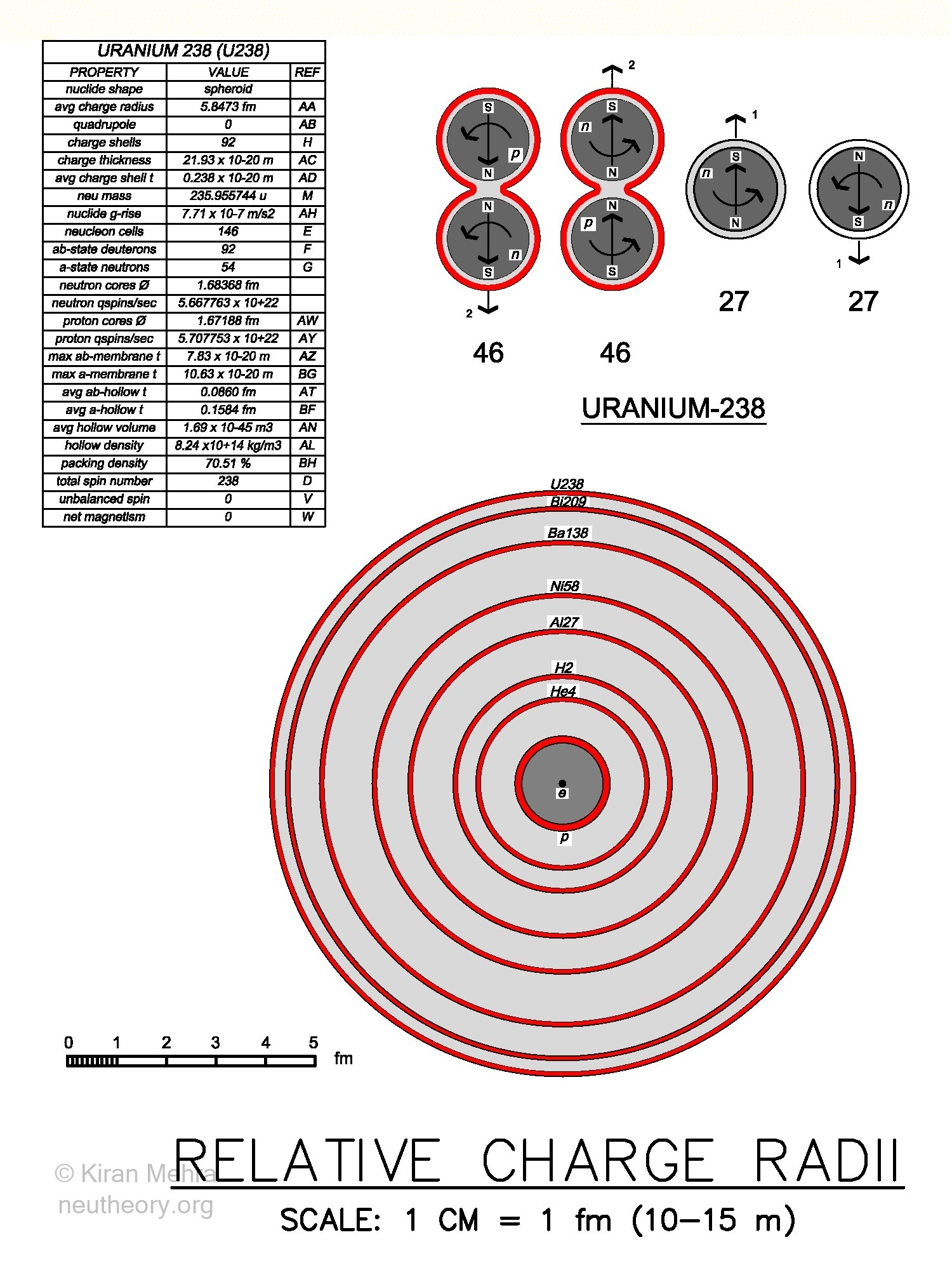 Figure 4.8 – Nuclide Charge Radii
Figure 4.8 – Nuclide Charge RadiiIn the center of the drawing, the small black dot is the electron (e-). The electron is the smallest stable object in nature, and with an estimated diameter of 0.1376 fm in this model, is noticeable at this scale. The electron has a one negative charge shell with a shield thickness of 0.01435 fm. All charge shield thickness (red rings) are graphically shown not to scale.
The circle, shaded dark grey for schematic clarity, with a red ring is the proton (p+) (1 charge shield) with an empirically determined diameter of 1.68368 fm. The positive charge shell of the proton is directly touching the spinning core. In other nuclides, the spinning cores never directly touch a charge shell, as they are always contained by non-spinning plasm and membranes. With the exception of the S1 surface of the free proton and the S2 surface of the free electron, the electric charge shield is always on the S3 surface(s) of a non-spinning neutral spheroid.
The next circle shaded light grey with a red ring (+2 charge shield) is the two deuteron cell alpha (He4, 2ab), the smallest nuclide in nature with a diameter of 3.362 fm. Even the (+1 charge shield) of the free one cell deuteron (H2, ab), with a diameter of 4.2848 fm, is larger than the alpha.
The next circle with a red ring (+13 charge shield), is the 14 cell cluster of Aluminum-27 (Al27, 13ab+a), with a diameter of 6.1054 fm. The next circle with a red ring (+28 charge shield)is the 30 cell cluster of Nickle-58 (Ni58, 28ab+2a), with a diameter of 7.549 fm. The next circle with a red ring (+56 charge shield) is the 82 cell cluster of Barium-138 (Ba138, 56ab+26a), with a diameter of 9.6782 fm. The next circle with a red ring (+83 charge shield) is the last stable isotope, the 126 cell cluster of Bismuth-209 (Bi209, 83ab+43a), with a diameter of 11.0508 fm.
The outermost circle with a red ring (+92 charge shield) is the last natural isotope, the 146 cell cluster of radioactive *Uranium-238 (U238, 92ab+54a), with a diameter of 11.6946 fm. *U238 has 46 deuterons and 27 neutrons that spin up, and 46 deuterons and 27 neutrons that spin down, making a net spin and magnetic field of zero. It is hard to imagine that these 146 cell volumes, shown approximately to scale in the drawing, can fit within the volume defined by a sphere with the 11.6946 fm diameter of *U238 plus its hills, but they do, and with a relatively long half life of 4.4 billion years. The packing density of the *U238 nuclide calculates to 70.51%.
While It is beyond the scope of this work to discuss nuclear structure in detail, one interesting question is how the 92 deuterons and 54 neutrons are distributed within the *U238 nuclide structure. Four possibilities are considered:
- A uniform distribution of deuterons and neutrons within the packing structure.
- A core of neutron cells surrounded by deuteron cells.
- A core of deuteron cells surrounded by neutron cells.
- Some combination of the above.
For smaller nuclides, the writer prefers possibility #2, i.e., a neutron cell or cells, surrounded by deuterons. See (Figure 4.10 – Three & Four Cell Clusters), (Figure 4.11 – Five Cell Clusters), (Figure 4.12 – Six Cell Clusters).
Once nuclides get larger, (Figures 4.13 – Carbon Isotopes) & (Figure 4.14 – Nitrogen Isotopes), the neutrons start to appear next to the charge surface. With Oxygen-18, (Figure 4.15 – Oxygen Isotopes) , the nuclide model suggests, that the 2 neutrons with the 8 deuterons, begin to protrude above the spherical charge radius floor. The charge shield just flows above the protrusions.
For larger nuclides, the writer intuitively prefers a combination of possibilities #1 & #3, i.e., a uniform crystalline distribution surrounded by a neutron shell.
It is hypothesized that galaxy cores are similar to nuclides, at a much larger scale (a neucleon supercluster), and develop neutron shells which are periodically ejected into space, parallel to the spin axis, during the active nuclei phase of the galaxy.
Nuclide Topology
After quantum b-state hydrogen-1, topologically contained ab-state hydrogen-2 and abb-state helium-3, all other stable atomic structures in nature, are electrically bonded (fused) clusters of ab-states and a-states only. It is hypothesized there are no b-states or abb-states in stable larger number nuclides.
The neucleon topology of nuclides through the second row of the periodic table is as follows:
(# = neucleon cluster number, a = neutron, b = proton, ab = deuteron, abb = helion, * unstable nuclide (radioactivity, lifetime))
#
– a = *free neutron (transition into b+ and e-,10 minutes)
– b = hydrogen-1 (H1) (the proton)
1 ab = hydrogen-2 (H2) (the deuteron)
1 abb = helium-3 (He3) (the helion)
2 ab+a = *hydrogen-3 (H3) (the triton) (electron emission into stable He3, 12.26 years)
2 ab+ab = helium-4 (He4) (α) (the alpha) (the smallest nuclide)
3 ab+ab+a = *helium-5 (He5) (neutron emission into He4, 7×10-22 seconds)
2 ab+abb = *lithium-5 (Li5) (positron emission into He4, 3×10-22 seconds)
3 ab+ab+ab = lithium-6 (Li6)
4 ab+ab+ab+a = lithium-7 (Li7) (the first nuclide with a stable neutron)
5 ab+ab+ab+a+a = *lithium-8 (Li8) (electron + 2 alpha into He4, 0.84 seconds)
4 ab+ab+ab+ab = *beryllium-8 (Be8) (2 alpha into He4, 7×10-17 seconds)
5 ab+ab+ab+ab+a = beryllium-9 (Be9) (the second nuclide with a stable neutron)
5 ab+ab+ab+ab+ab = boron-10 (B10)
6 ab+ab+ab+ab+ab+a = boron-11 (B11)
5 ab+ab+ab+ab+abb = *carbon-11 (C11) (positron emission into B11, 20 minutes)
6 ab+ab+ab+ab+ab+ab = carbon-12 (C12)
7 ab+ab+ab+ab+ab+ab+a = carbon-13 (C13)
8 ab+ab+ab+ab+ab+ab+a+a = *carbon-14 (C14) (electron emission into N14, 5730 years)
5 ab+ab+ab+abb+abb = *nitrogen-12 (N12) (96.5% positron emission into C12, 11×10-3 sec) (3.5% positron + alpha emission into *Be8)
6 ab+ab+ab+ab+ab+abb = *nitrogen-13 (N13) (positron emission into C13, 10 min)
7 ab+ab+ab+ab+ab+ab+ab = nitrogen-14 (N14)
8 ab+ab+ab+ab+ab+ab+ab+a = nitrogen-15 (N15)
7 ab+ab+ab+ab+ab+ab+abb = *oxygen-15 (O15) (positron emission into N15, 122 s)
8 ab+ab+ab+ab+ab+ab+ab+ab = oxygen-16 (O16)
9 ab+ab+ab+ab+ab+ab+ab+ab+a = oxygen-17 (O17)
10 ab+ab+ab+ab+ab+ab+ab+ab+a+a = oxygen-18 (O18) (the first nuclide with 2 stable neutrons)
9 ab+ab+ab+ab+ab+ab+ab+ab+ab = *fluorine-18 (F18) (positron emission or electron capture into O18, 110 min)
10 ab+ab+ab+ab+ab+ab+ab+ab+ab+a = fluorine-19 (F19)
10 ab+ab+ab+ab+ab+ab+ab+ab+ab+ab = neon-20 (Ne20)
11 ab+ab+ab+ab+ab+ab+ab+ab+ab+ab+a = neon-21 (Ne21)
12 ab+ab+ab+ab+ab+ab+ab+ab+ab+ab+a+a = neon-22 (Ne22)
The Architecture of Neucleon Clusters
We now look at how the neucleons in nuclides are architecturally put together. By architecture, we mean the specific arrangement of the constituent neucleon building blocks. Remarkably all stable, and most radioactive, nuclei are made from only two neucleon building blocks, the deuteron and the neutron. The third neucleon the helion serves a useful transitional purpose as a positron maker, but never remains as part of a stable atomic nuclide.
It is not within the scope of this works to provide a comprehensive description of all the 146 neucleon cluster numbers in nature. Eleven (11) of the 146 cluster numbers are missing. The intent of this work is to consider the principles that govern nuclear architecture, and to show some examples.
The complexity of modeling increases with larger cluster numbers. The scope of this work is limited to the smaller cluster numbers. The larger cluster numbers – representing the remaining naturally occurring elements – will need to be done using more sophisticated graphic software.
What also needs to be explained, is why 7 cluster numbers have no nuclides, and 4 cluster numbers have only radioactive nuclides.
Cluster Stability
Electric charge shell tension from g-fall is the reaction force that holds the multiple neucleons of a nuclide together. The charge shells can be imagined as spherical elastic “jackets” surrounding a g-rising neutral body.
Neu Theory has no standard unit for g-fall or charge shell tension. It is measured as a reaction force that is equal and opposite to nuclear g-rise, and adjusts itself automatically, until an equilibrium size of the neucleon cluster is reached.
The smallest stable nuclide g-rise, is the deuteron at 0.49×10-7 m/s2, less than the proton at 1.57×10-7 m/s2, but larger than the electron at 0.13×10-7 m/s2.
The largest stable nuclide g-rise, is Lead-208 at 7.61×10-7 m/s2. *Lead-209, with a g-rise just slightly larger at 7.62×10-7 m/s2 is unstable. Bismuth-209 with a g-rise at 7.58×10-7 m/s2, is the last stable isotope. All nuclear isotopes with a g-rise greater than Lead-208 are unstable. See (Neu Mass & Charge Radii Table – Column AH)
The neucleons in a cluster can be visualized as deformable eggs with hard spinning cores, that fit together as best as they can, with their malleable absolute density membrane surfaces completely touching each other, creating “double wall” polyhedral facets between cells. There is no space between the membrane walls and the charge shield. The neucleons adjust their shape as needed. The individual cell membranes contain a fixed amount of plasm matter which surrounds the spinning cores. Each cell has a g-rise caused by natural acceleration. The g-rise of all cells add together to create a g-rise of the cluster.
A key concept to consider is the density of the cells. The density of core and membrane Type I matter stays at an absolute 6.693 x 1017 kg/m3. This means that the specific volume they contribute to the overall nuclide size is fixed. The only way a neucleon can change size is by a change in the density of the plasm Type II matter. The free deuteron plasm has a density of 3.85 x 1013 kg/m3. The free helion plasm has a density 5.75 x 1013 kg/m3. The neutron neucleon plasms take on the density of their nuclides.
All cluster plasm’s have a density greater than the free neucleons. The least dense stable plasms are with Lithium-6 at 7.65 x 1013 kg/m3. The densest stable plasms are with Lead-208 at 96.76 x 1013 kg/m3.
As more cells add their mass together creating a greater g-rise pressure, and as more charge shells are added to the g-fall of the charge shield the cell plasm of each neucleon compresses into a denser substance. The plasm of every cell in a cluster, deuteron or neutron, is hypothesized to have the same mass, density and volume.
We will now examine some smaller number cell clusters, representing the atoms of hydrogen, helium, lithium, beryllium, boron, and carbon. We shall also look at graphic model images of carbon, nitrogen and oxygen isotopes. It should be noted that due to modeling complexity the polyhedral neucleon membrane wall facets and seams are not shown in the graphic images, which are otherwise shown to scale. The charge shield which is always present is not shown in some diagrams.
Two Cell Clusters
*Hydrogen-3 – *H3 (ab+a) (Figure 4.5 – Neutron Synthesis). The triton is the synthesis of the first neutron neucleon. The triton is a deuteron and a neutron below a common one charge shell shield. The triton is unstable with a half-life of 12.26 years. There are no tritons in multi neucleon clusters, only deuterons and neutrons.
Helium-4 – He4 (ab+ab) (Figure 4.9 – Helium 4 – The Alpha). The alpha is the fusion of two deuterons below a two charge shell shield. One deuteron spins up and one deuteron spins down, making a net spin and magnetic moment of zero. The 2 cell, 4 core alpha, is one of nature’s most stable structures. The alpha is a preferred method of fission from radioactive nuclides.
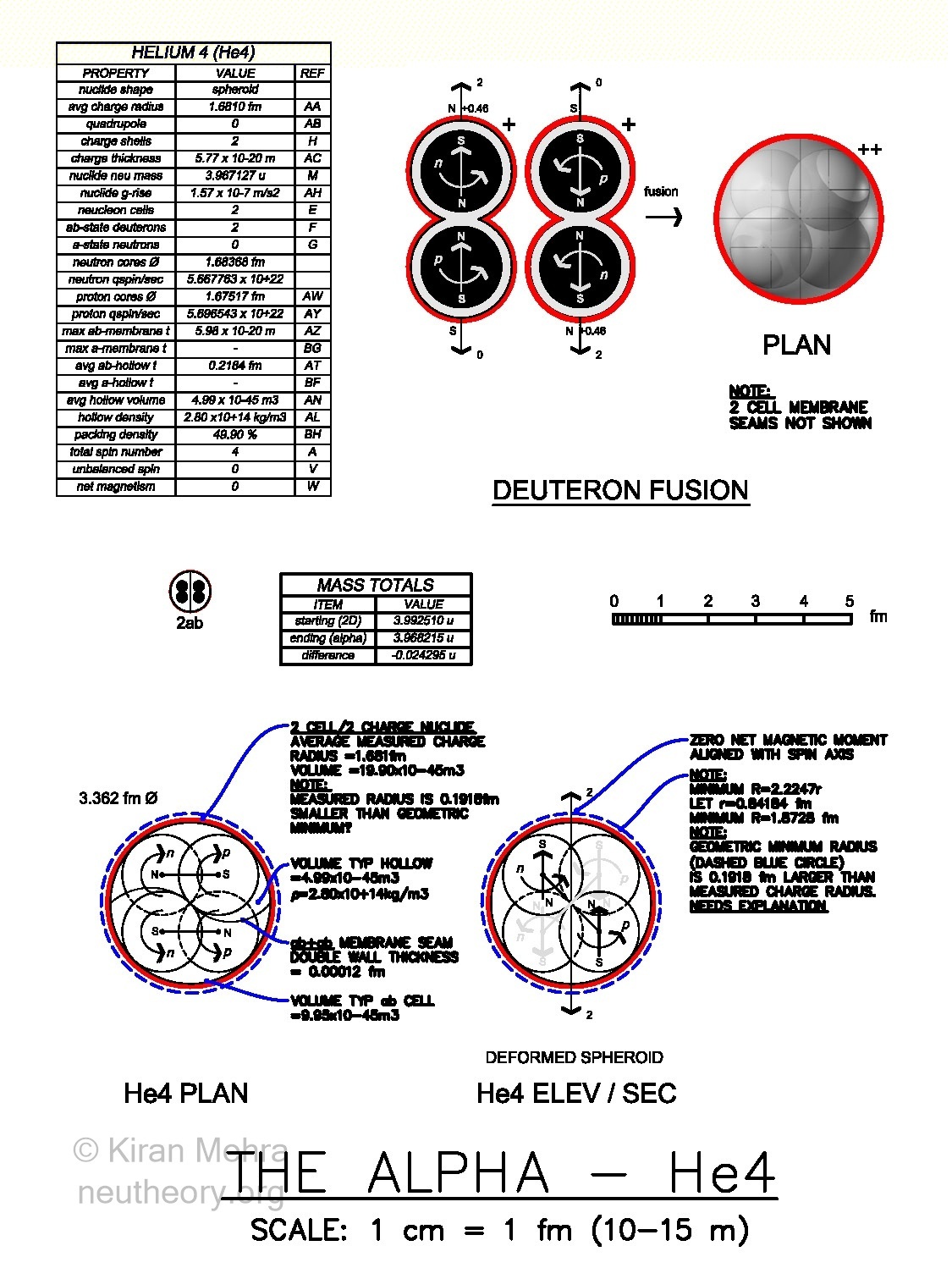 Figure 4.9 – Helium 4 – The Alpha – Two Neucleon Cell Cluster
Figure 4.9 – Helium 4 – The Alpha – Two Neucleon Cell ClusterOne “fact of experience” that needs to be explained, is that the measured charge radius of the alpha, is smaller than the geometric minium packing radius for the four balls with a specific size. There is no measured evidence of a quadrupole indicating a shape different then a sphere.
Neu Theory hypothesizes that the measured charge radius of He4 at 1.681 fm represents the size of the spherical neucleonic membrane floor analogous to “sea level.” The membrane has a surface geography with four equal “islands” or “hills” in a tetrahedral configuration that rise above the sea level floor. The height of the “hill rise” represents the distance from the membrane floor to the geometric minimum radius of 1.8725 fm. These hills are parts of the four cores that protrude 0.1915 fm above the spherical floor. This is more than 11% of the charge radius. It is hypothesized that the +2 charge shield just “flows” over and above the hilly parts of the neutral nuclide surface, similar to a stretchable material with a uniform thickness.
The charge shielded neucleon clusters hypothesis maintains, that the +2 alpha charge shield will deform as it stretches, following the hill surfaces of any nuclide as it needs to. It is speculated, that with the surface geography of all nuclides, there are only hills, no depressions.
The calculated thickness of the +2 alpha charge shield is 5.77 x 10-20 m. The average thickness of each of the two alpha charge layers is 2.88 x 10-20 m. The thinnest stable charge layers in nature, are with the 83 deuterons of Bismuth-209, with an average at 0.267 x 10-20 m making a total +83 charge shield thickness of 22.18 x 10-20 m. All charge layers thinner than Bi209 are unstable. A natural limit seems to have been reached.
*Lithium-5 – Li5 (not shown) is the two cell fusion of one deuteron and one helion below a +3 charge shield. *Li5 is highly unstable and is not found in nature. The -3 spin indicates that both the deuteron and the helion spin down. The net magnetic moment of Li5 has not been measured. Within an estimated 3 x 10-22 seconds, *Li5 will emit a positron becoming stable He4.
Three Cell Clusters
*Helium-5 – *He5 (not shown) is the fusion of two deuterons and one neutron below a +2 charge shield. The -3 net spin indicates that both deuterons spin down and the neutron spins up. The magnetic moment has not been measured. Just like *Li5, *He5 is highly unstable. Within an estimated 7 x 10-22 seconds, *He5 will emit a neutron becoming stable He4. The extreme instability of *Li5 and *He5 is the reason the mass number 5 is not found in nature.
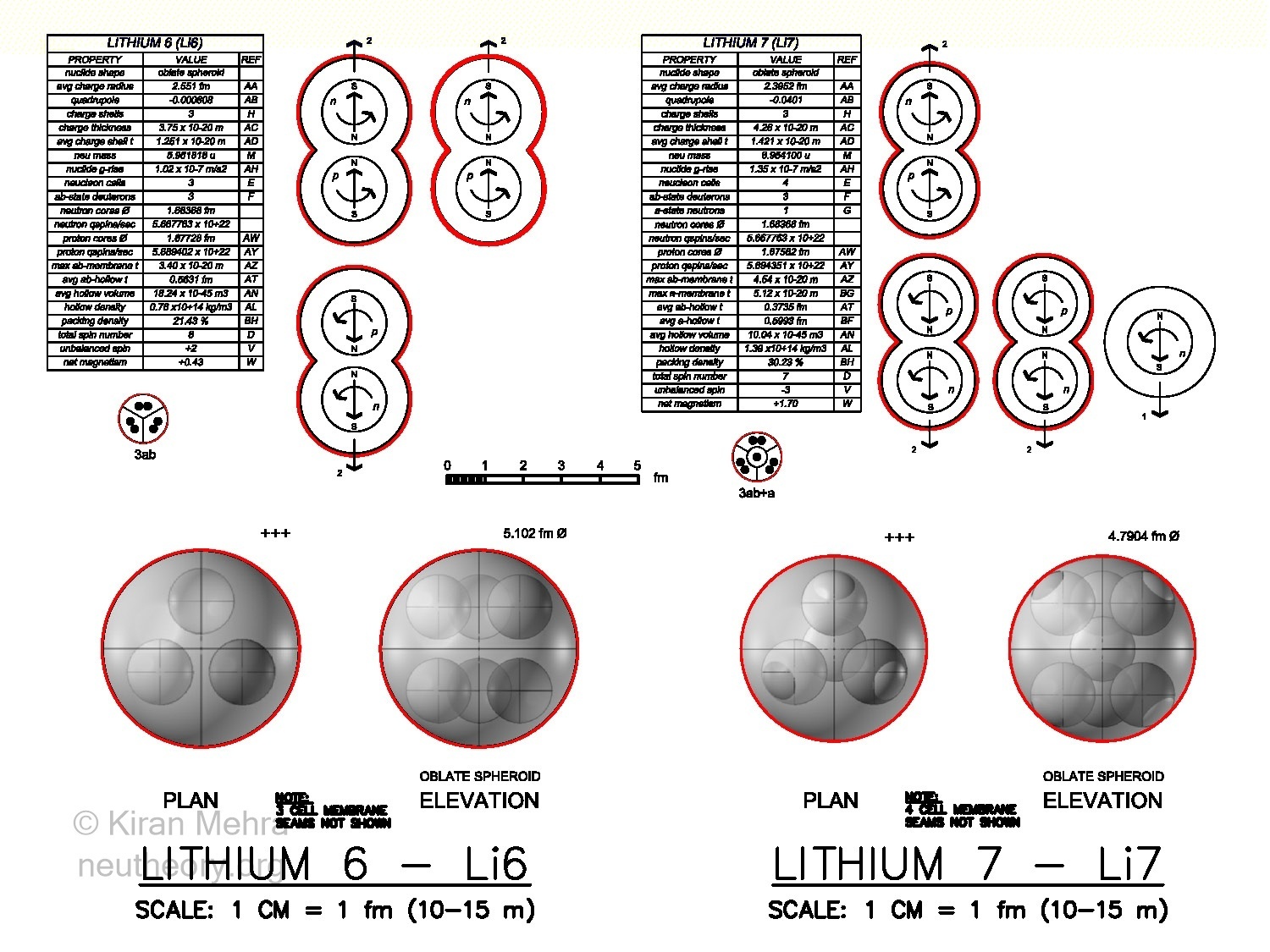 Figure 4.10 – Three & Four Cell Clusters
Figure 4.10 – Three & Four Cell ClustersLithium-6 – Li6 (Figure 4.10 – Three & Four Cell Clusters), is the fusion of three deuterons below a +3 charge shield. Two deuterons spin up and one deuteron spins down, making a net spin of +2. There is a net magnetic moment of +0.43u. The negative quadrupole value indicates an oblate (disk shape) spheroid. The neucleonic hollow plasm of Li6, at 7.65 x 1013 kg/m3, is the least dense plasm of all the nuclides. The three deuterons completely fit below the neucleonic membrane surface, without any hills protruding above the spherical floor. Li6 is the only nuclide without hills. All nuclides after Li6 have some hills.
Four Cell Clusters
Lithium-7 – Li7 (Figure 4.10 – Three & Four Cell Clusters), is the fusion of three deuterons with one neutron below a +3 charge shield. One deuteron spins up and two deuterons and one neutron spin down, making a net spin of -3. There is a net magnetic moment of +1.7u. The negative quadrupole value indicates an oblate spheroid with 6 hills. The neutron finds a comfortable place in the center of the nuclide surrounded by the three deuterons. Li7 contains the first stable neutron neucleon in nature.
*Beryllium-8 = *Be8 (not shown) is the fusion of four deuterons below a +4 charge shield. Two deuterons spin up and two deuterons spin down, making a net spin and magnetic moment of zero. *Be8 is highly unstable and will fission into two alphas in 7 x 10-17 seconds. The instability of *Be8 and *Li8 is the reason the mass number 8 is not found in nature. The nuclear architecture of *Be8 has not been determined.
Five Cell Clusters
*Lithium-8 – *Li8 (not shown) is the fusion of three deuterons and two neutrons below a +3 charge shield. The +4 net spin indicates that either: three deuterons spin up and two neutrons spin down; or two deuterons and two neutrons spin up and one deuteron spins down. There is a net magnetic moment of +0.86u. *Li8 is moderately unstable and in 0.84 seconds will emit a positron, briefly becoming Be8, which quickly fissions into two alphas. This is the reason mass number 8 is not found in nature. The nuclear architecture of *Li8 has not been determined.
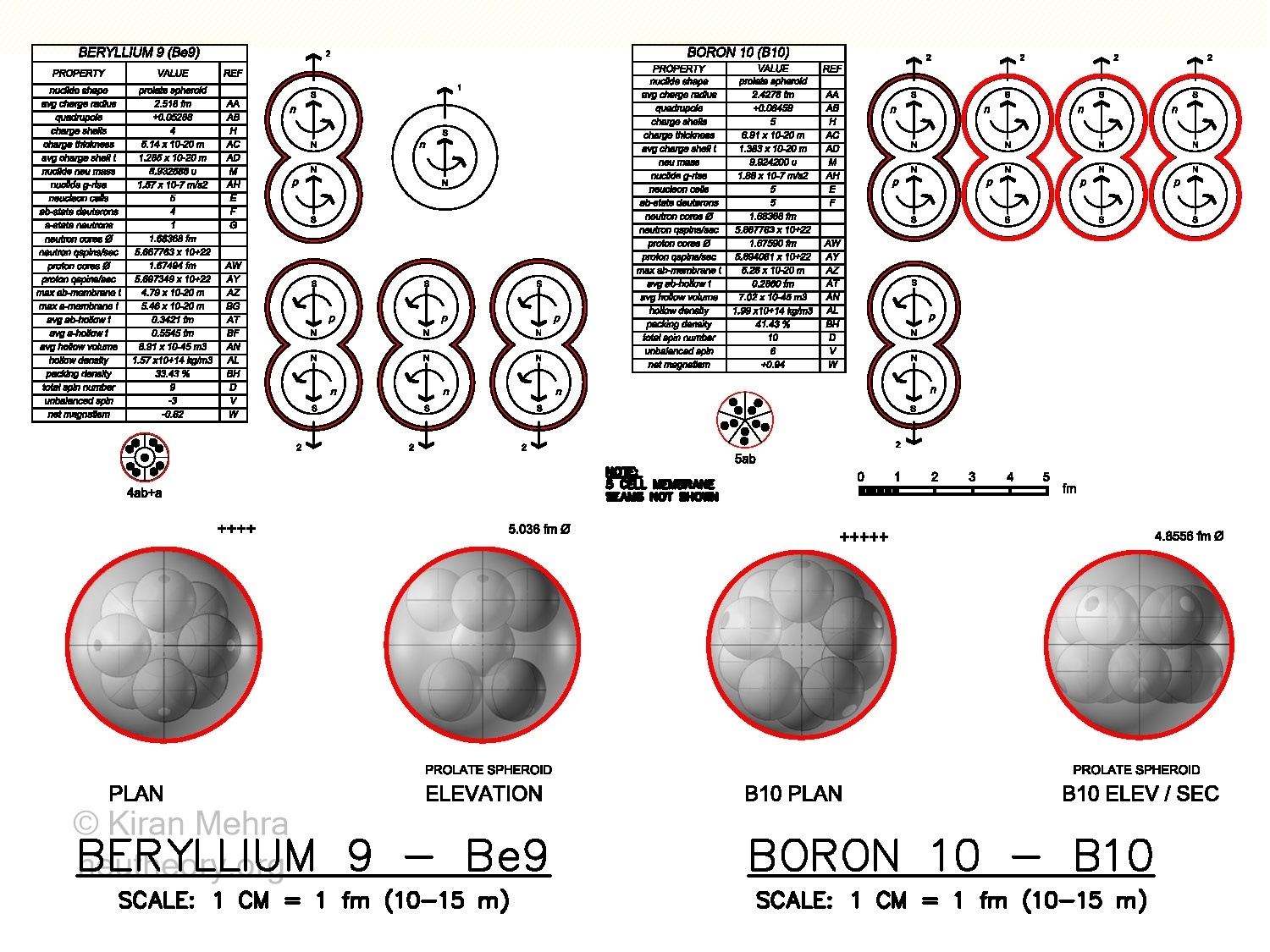 Figure 4.11 – Five Cell Clusters
Figure 4.11 – Five Cell ClustersBeryllium-9 – Be9 (Figure 4.11 – Five Cell Clusters), is the fusion of four deuterons and one neutron below a +4 charge shield. One deuteron and one neutron spin up, and three deuterons spin down, making a -3 net spin. There is a net magnetic moment of -0.62u. The positive quadrupole value indicates a prolate (cigar shape) spheroid with 8 hills. The neutron stays in the center. Be9 contains the second stable neutron neucleon in nature.
Boron-10 – B10 (Figure 4.11 – Five Cell Clusters), is the fusion of five deuterons below a +5 charge shield. Four deuterons spin up and one deuteron spins down, making a net spin of +6. There is a net magnetic moment of +0.94u. The positive quadrupole value indicates a prolate spheroid with ten hills. The five deuterons create a ring shape with a hole in the middle.
*Carbon-11 – Radioactive *C11 (not shown) is the fusion of four deuterons and one helion below a +6 charge shield. One deuteron and one helion spin up and three deuterons spin down, making a -3 net spin. There is a net magnetic moment of -0.50u. *C11 will emit a positron with a +1 charge shell, or capture an electron with its -1 charge shell in ∼20 minutes becomes stable B11 with a +5 charge shield. The nuclear architecture of *C11 has not been determined.
*Nitrogen-12 – Radioactive *N12 (not shown) is the fusion of three deuterons with +1 charge shield each, and two helions with +2 charge shields each below a single +7 charge shield. Two deuterons and one helion spin up, and one deuteron and one helion spin down, making a +2 net spin. The net magnetic moment is not available. *N12 will emit a positron with a +1 charge shell in 11 x 10-3 seconds to become stable C12 with a +6 charge shield; or will emit a positron with a +1 charge shell, and an alpha with a +2 charge shield, becoming *Be8 with a +4 charge shield, which then will quickly become two alphas with +2 charge shields each. What is interesting is that *N12 is the first instance of two helions in a nuclide. The nuclear architecture of *N12 has not been determined.
Six Cell Clusters
Boron-11 – B11 (Figure 4.12 – Six Cell Clusters), is the fusion of five deuterons and one neutron below a +5 charge shield. Two deuterons spin up, and three deuterons + one neutron spin down, making a -3 net spin. There is a magnetic moment of +1.41u. The positive quadrupole value indicates a prolate spheroid with ten hills. The ring shape is filled with a neutron. B11 contains the third stable neutron neucleon in nature.
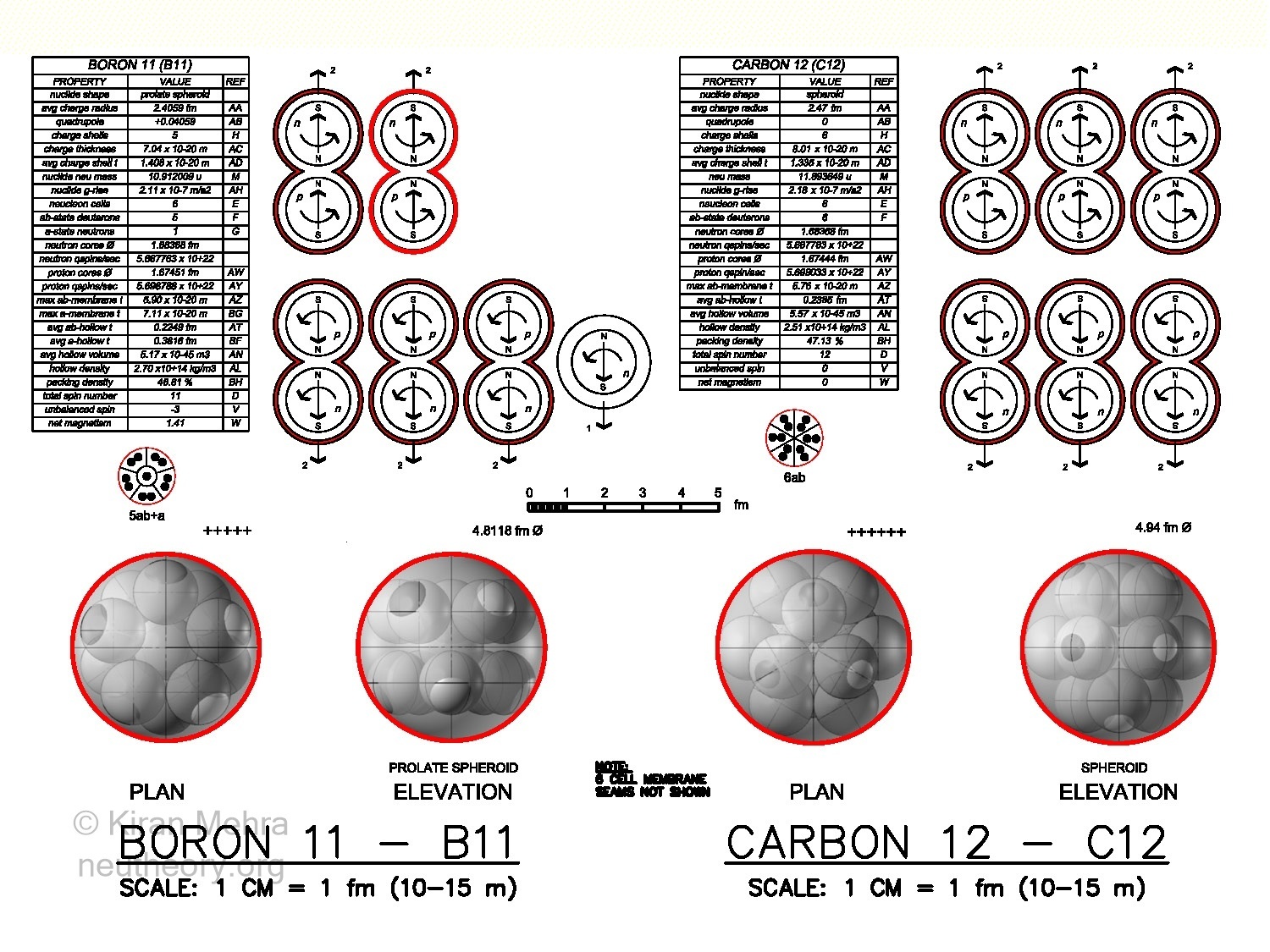 Figure 4.12 – Six Cell Clusters
Figure 4.12 – Six Cell ClustersCarbon-12 – C12 (Figure 4.12 – Six Cell Clusters), is the fusion of six deuterons with a +1 charge shield each below a single +6 charge shield. Three deuterons spin up and three deuterons spin down, making a net spin and magnetic moment of zero. C12 has no quadrupole so it can be considered a spheroid with 12 hills.
*Nitrogen-13 – *N13 (not shown) is the fusion of five deuterons with +1 charge shield each, and one helion with a +2 charge shield below a single +7 charge shield. Two deuterons and one helion spin up, and three deuterons spin down, making a -1 net spin. There is a net magnetic moment of +0.17u.* N13 will emit a positron in 10 minutes to become stable C13. The nuclear architecture of *N13 has not been determined.
Carbon Isotopes
(Figure 4.13 – Carbon Isotopes), shows three carbon isotopes. The six cell Carbon12 and the seven cell Carbon13 are both stable. The eight cell *Carbon14 is unstable. All three isotopes are spheroids with 12 hills.
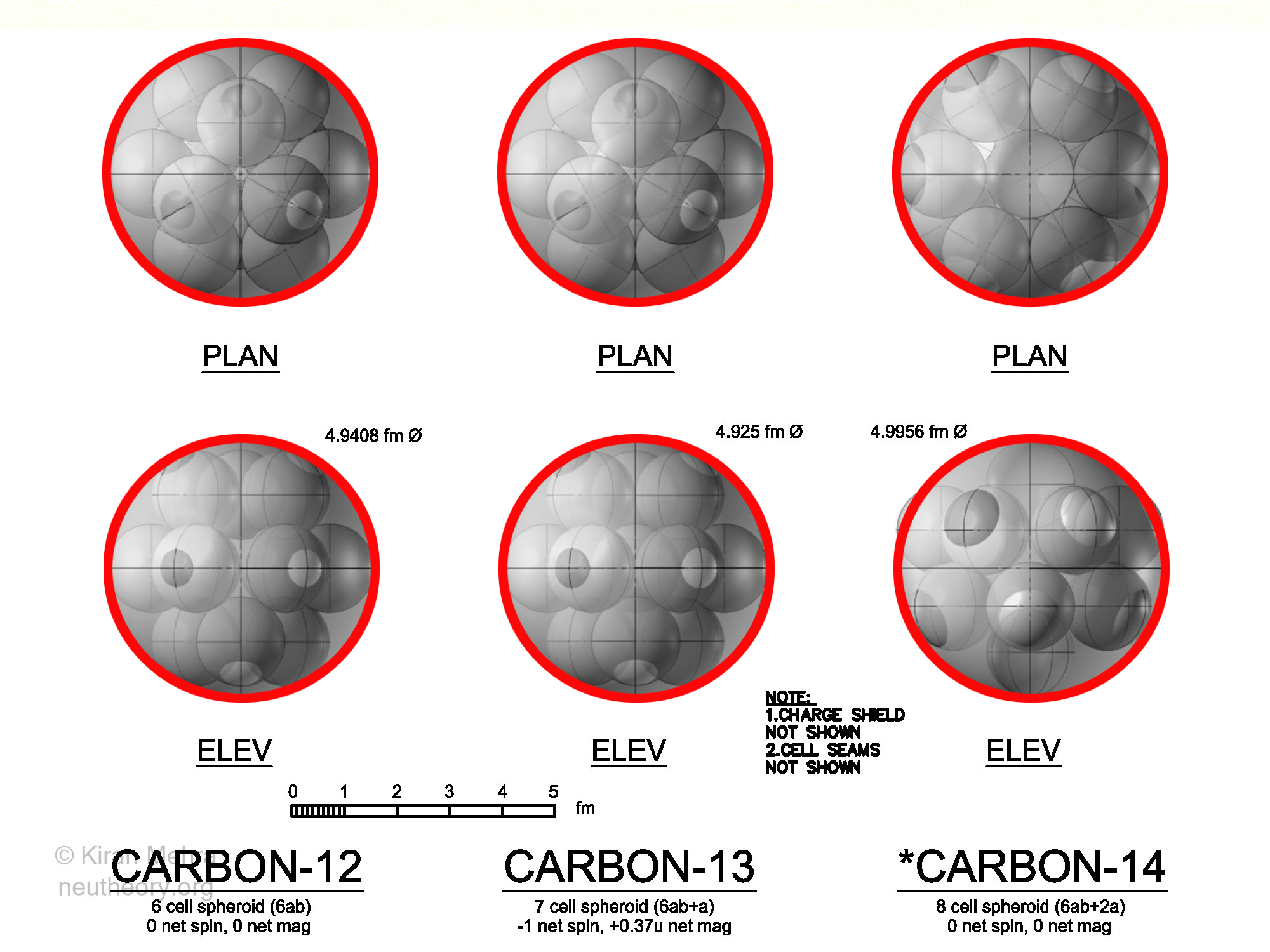
The seven cell Carbon13 is just a C12 nuclide with a neutron in the middle, the architecture of the six deuterons in both nuclides is considered similar.
The eight cell radioactive *Carbon14 has two neutrons in the middle making the six deuterons take on a ring shape. The two neutrons don’t protrude above the neucleonic surface. *C14 is fairly long lived isotope with a half life of 5,730 years emitting an electron to become stable Nitrogen14 with seven deuterons. The magnetic moment is not known
Nitrogen Isotopes
(Figure 4.14 – Nitrogen Isotopes), shows the two stable nitrogen isotopes.
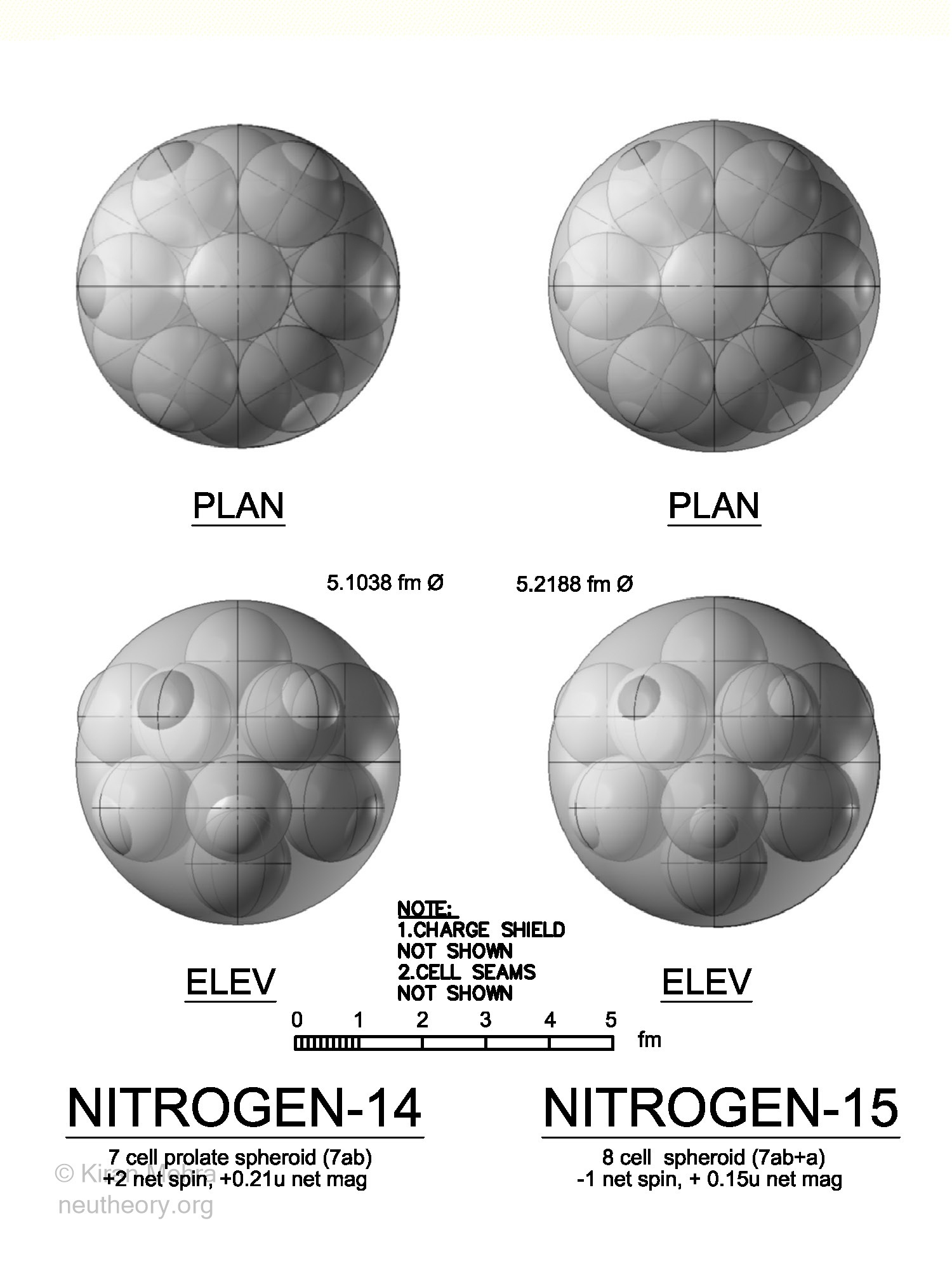 Figure 4.14 – Nitrogen Isotopes
Figure 4.14 – Nitrogen Isotopes
The seven cell Nitrogen14 cluster has six deuterons in a ring shape with spins that balance, with the seventh deuteron spin up in the middle, making a +2 net spin. There is a net magnetic moment of +0.21u. A positive quadrupole value indicates a prolate spheroid with 12 hills.
The eight cell Nitrogen15 is a Nitrogen14 nuclide with the addition of one neutron in the middle with the deuteron. The -1 net spin implies that four deuterons are spin down, and three deuterons and the neutron are spin up. There is a net magnetic moment of +0.15. Nitrogen15 has no quadrupole so it is assumed as a spheroid with 12 hills. The deuteron and neutron in the center of the nuclide don’t protrude above the neucleonic surface.
Oxygen Isotopes
(Figure 4.15 – Oxygen Isotopes), shows the three stable oxygen isotopes.
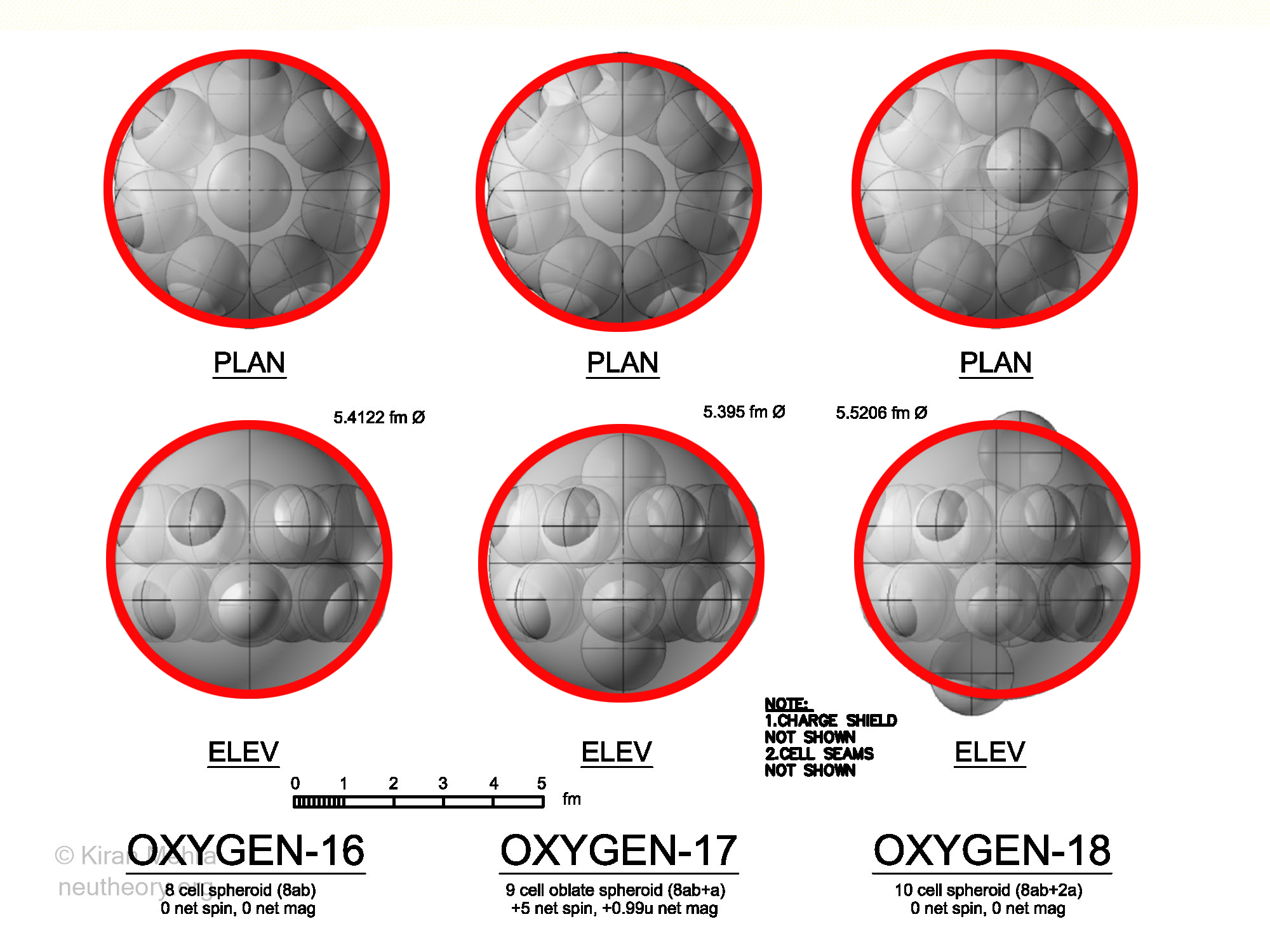
The eight cell Oxygen16 has seven deuterons in a ring shape with the eighth deuteron in the middle. Four deuterons spin up, and four deuterons spin down, making a net spin and magnetic moment of zero. O16 has no quadrupole so it is assumed to be a spheroid with 14 hills.
The nine cell Oxygen17 has an additional neutron in the middle. The +5 net spin implies that five deuterons and one neutron are spin up, and three deuterons are spin down. There is a negative quadrupole so the shape is assumed as a oblate spheroid with 14 hills. There is a net magnetic moment of +0.99u.
The ten cell Oxygen18 has two additional neutrons in the middle. Four deuterons and one neutron spin up, and four deuterons and one neutron spin down, making a net spin and magnetic moment of zero. O18 has no quadrupole so it has the shape of a spheroid with 16 hills. What is interesting that the packing geometry forces the neucleonic membranes of the two neutrons in the middle to protrude significantly above the spheroidal surface, making them higher than the 14 other hills, yet remarkably, the nuclide remain stable. O18 is the first stable nuclide with two neutrons.
The Missing Cluster Numbers
Clusters with up to 146 cells have been found in nature. Clusters with up to 126 cells are with the stable isotopes (Pb208 and Bi209). Clusters with 127 cells and above are with the radioactive isotopes. However there are some cell collections that are missing:
- There are no nuclides with 19, 35, 39, 61, 89, 115, and 139 cells.
- Cluster numbers 45 (*Rubidium-82), 87 (*Samarium-149), and 123 (*Lead-205) exist, but are all radioactive.
- Cluster number 145 is only found with man made radioactive *Plutonium-239.
See Neu Mass & Charge Radii Table – Column E for the cluster number of nuclides.
It is outside the scope of this work to investigate why these cluster numbers do not exist. They represent ~7.5% of the total cluster numbers, which is a significant fraction. One can only speculate that the packing geometry of these numbers just doesn’t work.
What the missing numbers have in common is that they are all odd numbers.
As an example, consider the first missing cluster number, 19. There are stable 18 and 20 cell clusters on each side. There are three potential candidates for a nuclide with 19 cells. These are Sulfur-35 (16ab+3a), Chlorine-36 (17ab+2a), and Argon-37 (18ab+1a). None of these isotopes exist in nature.
Sulfur-34 (16ab+2a) and Sulfur-36 (16ab+4a); Chlorine-35 (17ab+1a) and Chlorine-37 (17ab+3a); and Argon-36 (18ab) and Argon-38 (18a+2a) all exist and are stable nuclides. What is common to these stable isotopes, is that the neutron number always increases by two, never one. For some reason, the packing geometry requires the addition of 2 neutrons. This seems to apply for other missing cell cluster numbers. If only the addition of one neutron was acceptable in these situations, there would be no missing cluster numbers.
Just to be clear, the addition of only one neutron at a time making a series of stable isotopes, is a common event in nature, there is no rule that says two neutrons must be added at one time for packing stability.
The Positron
The positron is one of nature’s “exotic” creations. It has only one purpose in its brief lifetime, and it does that very well. The positron is nature’s electron killer. It is made for a one way suicide mission so nature’s books can remain balanced.
Left alone, the positron is stable, not in the least bit radioactive, however unfortunately for it, unless kept confined in a magnetic bottle, there is no other place for it to hide in a universe filled with electrons. Moments after its emission it will meet an electron and mutual annihilation will take place.
The positron was officially discovered and named by Carl D. Anderson in 1932. It was seen in photographs of cosmic rays passing through a cloud chamber. The positron became to be considered a positively charged electron and a form of anti-matter.
Neu Theory does not consider the positron as a form of antimatter, or a positive electron. The stuff the positron is made from, is just ordinary Type I spinrise matter, taken from ordinary proton cores. The positron, also, does not have the 2 surface topology of a membrane shell, as does the electron. However, the positron does serve the same purpose as antimatter, as the net result after electron/positron annihilation is that two electron size masses have been de-linked into their component spin and rise movement/energy forms. Matter and charge have been converted into free energy.
Despite the importance of its role in nature, the positron is considered by Neu Theory as an exotic particle, not a elementary form of nature. The elementary form is core spinrise.
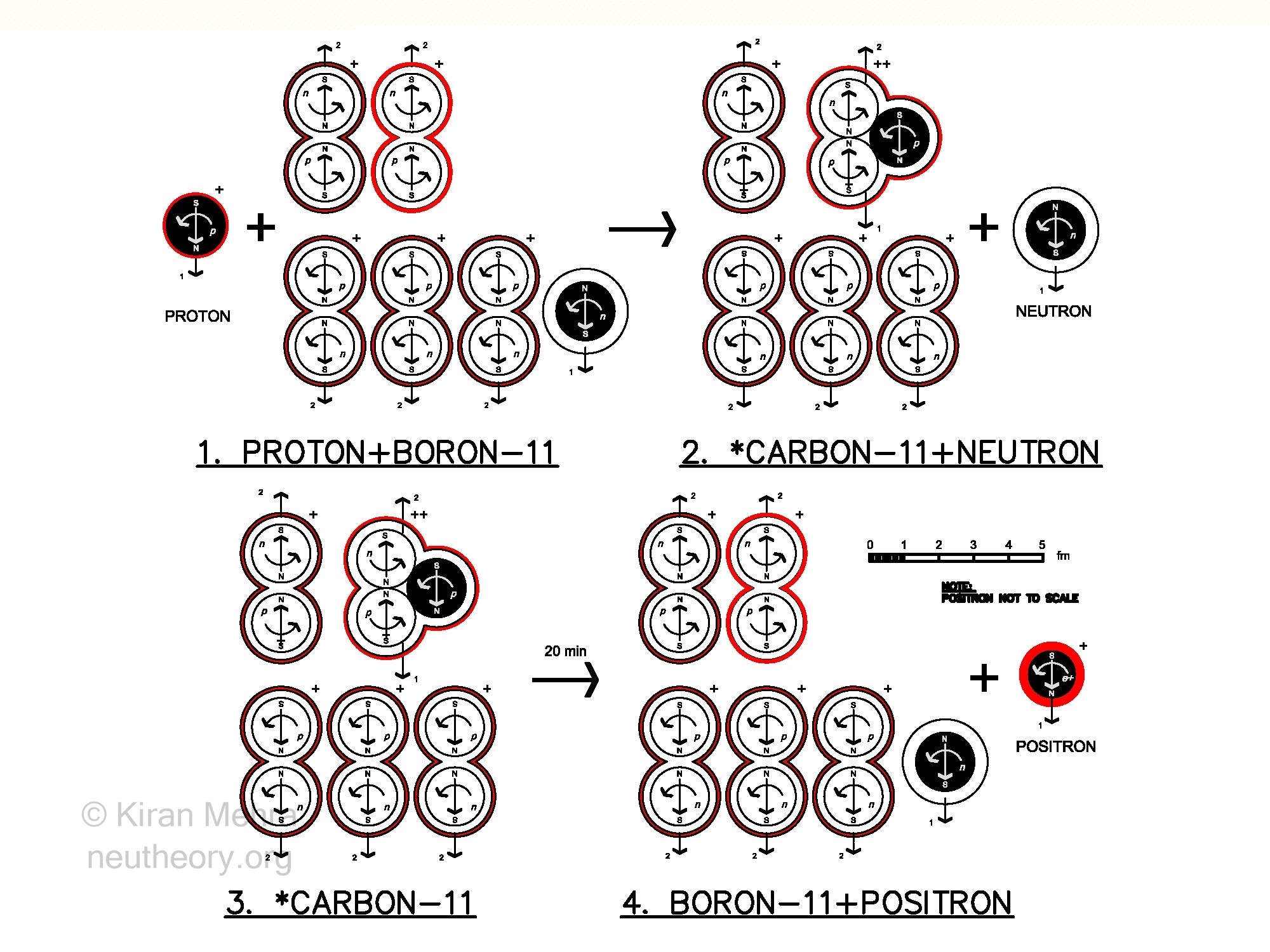 Figure 4.16 – Positron Emisson
Figure 4.16 – Positron Emisson(Figure 4.16 – Positon Emission), shows one method by which positrons are created. In general, it is hypothesized that positrons are made from the radioactive decay of helion neucleons, which are unstable in nuclides. The helions themselves are created by proton bombardment of nuclides:
- (Figure 4.16.1) A high energy (6 MeV) spin down proton strikes a Boron11 target. B11 has a mass of 10.914718u, and a +5 charge shield.
- (Figure 4.16.2) The proton is captured by a nuclide deuteron making a helion, and the solitary spin down neutron is ejected. Radioactive *Carbon11 has been created with a mass of 10.916825u, and a +6 charge shield. This represents a total increase in nuclide mass of 0.002107u. The 5 captive protons of B11 had a mass of 0.982400u each, and the 6 captive protons of *Carbon11 now have a mass of 0.985593u each, an increase of 0.003193u per proton. It is hypothesized that the rise energy increase comes from the kinetic energy of the colliding proton, and the spin energy increase comes from a change in nuclide size. The charge radius of Boron11 is 2.4069 fm and the charge radius of *Carbon11 is 2.4600 fm, an increase of 0.0059 fm.
- (Figure 4.16.3) *Carbon11 has a half life of about 20 minutes.
- (Figure 4.16.4) Through an internal nuclear process the captured helion proton becomes a neutron, remaking Boron11, and a positron with a +1 charge shell is emitted.
The net result of this whole process, is that the universal neutral number has been increased by one. The universal electric number has not as yet decreased by one, because a +1 charge shell is now being carried by the emitted positron, and there is an extra -1 charge shell with an existing electron. Only after electron/positron annihilation will the universal electric number decrease and the cosmic books become balanced.
During the *Carbon11 transition to Boron11 + a positron, 3 surfaces are created that were not there before. Two surfaces (S2/S3 containing 0.000544u of mass) make a fresh neutron cell membrane within the nuclide, dividing the helion into a deuteron plus a neutron. One surface (S1 ball containing 0.000544u of mass), encloses the spinning matter body of the positron that is emitted from the nuclide, and carries one of the nuclide’s positive electric charge layers. Also freshly synthesized, is 0.000833u of plasm Type II matter required to complete the neutron cell. The mass of the positron is exactly equal to the electron’s mass.
All the mass used by this nuclear redistribution event is hypothesized to come only from the captive proton cores of the *C11 nuclide which are equally reduced in mass (from 6 cores @ 0.985593u each, to 5 cores @ 0.982400u each). The neutron cores of both nuclides, remain unaffected during this redistribution of mass, staying at a constant 0.998623u of mass each.
With positron emission, the 3 newly created surfaces topologically unbalance the universe, violating the rules of number and form which nature will not accept, until the positron meets an electron. Mutual annihilation takes place, and the balance to nature is restored.
The positron is an electron killer by destroying the electron’s -1 charge shell with its own +1 charge shell, not anti-matter in the traditional sense, as it is made of the same Type I spinrise matter as the electron and the proton. This is the only method in nature by which the otherwise indestructible electron can be destroyed.
The positron is a destroyer of surfaces, and in the process de-links matter into energy. Its positive S1 surface somehow interacts with the negative S2/S3 surfaces of an electron, and all 3 surfaces are destroyed. Perhaps the topology of the positron ball and the electron hole is enough. However, the total number of surfaces in the universe, before positron emission, and after positron/electron annihilation now become the same.
The positron is a special temporary event in nature where two opposite electric charge shells surround equal mass objects. After mutual annihilation, the potential energy of the electric field is completely reduced by the destruction of the charge shells. Not only are the charge shells gone, but also de-linked into energy are the two 0.000544u quanta spinning balls of spinrise matter. The three surfaces of the positron and electron objects disappear, and the matter they contained now become de-linked energy, as two 0.511 meV gamma rays of free spin energy heading in opposite directions; plus two 0.511 meV expanding and diffusing-in-place zomon bursts of free rise energy.
With the act of electron/positron annihilation, nature has addressed two imbalances caused by the synthesis of a neutron in an atomic nucleus from captive proton matter. The first imbalance is an increase in the universal neutral number, without a corresponding decrease in the universal electric number. The second imbalance, is the addition of three new surfaces, a S1 surface with the ejected positron, and the S2-S3 surfaces which remain with a newly created neucleonic cell membrane in the nuclide.
After positron/electron annihilation, topologically, what were once the S2-S3 surfaces of a free electron, have been replaced by the S2-S3 surfaces of a neutron cell membrane bound within a nuclide. In the case of *Carbon-11 to Boron-11, an abb-state has become an ab-state + a-state.. The laws of number and form are thus conserved.
Exotic Particles
The positron is a “particle” that is created for a specific purpose by nature. However, there are other “exotic” particles, that are made during high energy matter collisions, that seem to have no specific purpose, except to absorb and redistribute the energies involved.
During collisions, between cosmic rays (high velocity ions) and atmospheric atoms, and man made collisions during particle accelerator experiments, core Type I matter fragments into multiple Type I matter pieces.
Type I matter is at an absolute density hence the total volume is conserved as the total volume of the individual pieces is equal to the original volume, less any mass volume that may have de-linked into free energy.
As core matter is considered an extremely dense homogenous liquid like substance, it is speculated that the pieces are not jagged, but more like “drops”. It is hypothesized, that the number of drops depends on the energy (momentum transfer) of the collision. The size of the pieces is considered random. It is not known if pieces smaller than electron mass can be formed.
Every time a proton core fragments, its positive electric charge shell can only envelop one matter drop, which Neu Theory considers as maintaining the primal topological S1 surface, that in principle cannot be destroyed. All the other drops, become multiple quantum spinning matter balls, with new S1 surfaces without a charge shell that are directly exposed to space. Normally, spinning matter surfaces are enveloped by plasm as in a nuclide or the charge shell that surrounds a spinning proton or a spinning electron.
All matter fragments are hypothesized with a spin/magnetic polarity similar to the proton, and with a magnetic strength inversely proportional to their quantum spin.
In principle, none of the matter drops, except one, can have a charge shell and electric field. In the Neu Theory model, and historically (until the “quark” hypothesis came up with -1/3, +2/3 fractional charge concept), electric charge is a fundamental quantity that cannot be further subdivided.
None of the drops are considered fundamental objects in their own right, they are just random pieces of broken primal core matter, that only momentarily exist before they merge back into some other primal cores. With fragmentation, large numbers of extra S1 surfaces are formed, creating a topological imbalance in nature, specifically that there be an equal number of S1, S2, S3 surfaces. Nature sees to it that all these extra S1 surfaces quickly join some primal S1 surfaces, bringing the cosmic S1 number back to N.
Neu theory hypothesizes, that under extreme conditions, both the positive charge shell of the proton, and the negative charge shell of the electron, can be detached from their respective matter surfaces and made to envelope other pieces of matter, albeit only temporarily.
For example, the “muon”, discovered by Anderson in 1936 in cosmic ray tracks, is an object with a negative charge that has 207 times the mass of an electron. The muon is unstable and will radioactively decay into an ordinary electron.
In 1975 Martin Perl, during particle accelerator collisions, discovered an object with a negative charge that had 3,500 times the mass of an electron. This object, called the “tauon” is even more unstable, and will decay into an electron or a muon, which will then decay into an electron.
Good questions to ask are: Does the negative electric charge shell of the tauon actually surround a matter ball with the inertial mass of almost 2 cores (∼1.9u)? If so, where does this much absolute spinrise matter come from, albeit briefly? The quantity of matter in nature and its distribution is fixed. If it is spinrise, this much can only come from the merging of cores, which would violate the rules of number and form. The tauon’s unstability is reassuring.
What is important to keep in mind, is that irrespective of the mass of the object that a positive or negative charge shell may envelop, it is the same ordinary Type I spinrise matter of nature, just a different amount. A difference in mass does not make the matter in these objects special. Eventually, after all the effects of the collisions have ended, and the energy has been dissipated, what is left are the ordinary neucleons, protons, and electrons of nature, with the cosmic number unchanged
Muonic Atoms
In current science, a muonic atom is a nuclide whose electrons have been replaced by muons. For example, muonic hydrogen is a proton with a muon orbital instead of an electron.
The lifetime of muonic hydrogen is the same as the muon itself, a brief ∼2.2×10-6 seconds.
Despite this short lifetime, muoinc hydrogen allows for a more accurate measurement of the charge radius of the proton. This has a fundamental significance as the size of the proton is a measure of absolute density.
